积分方法大盘点
现把我们学了的积分方法做个大总结。
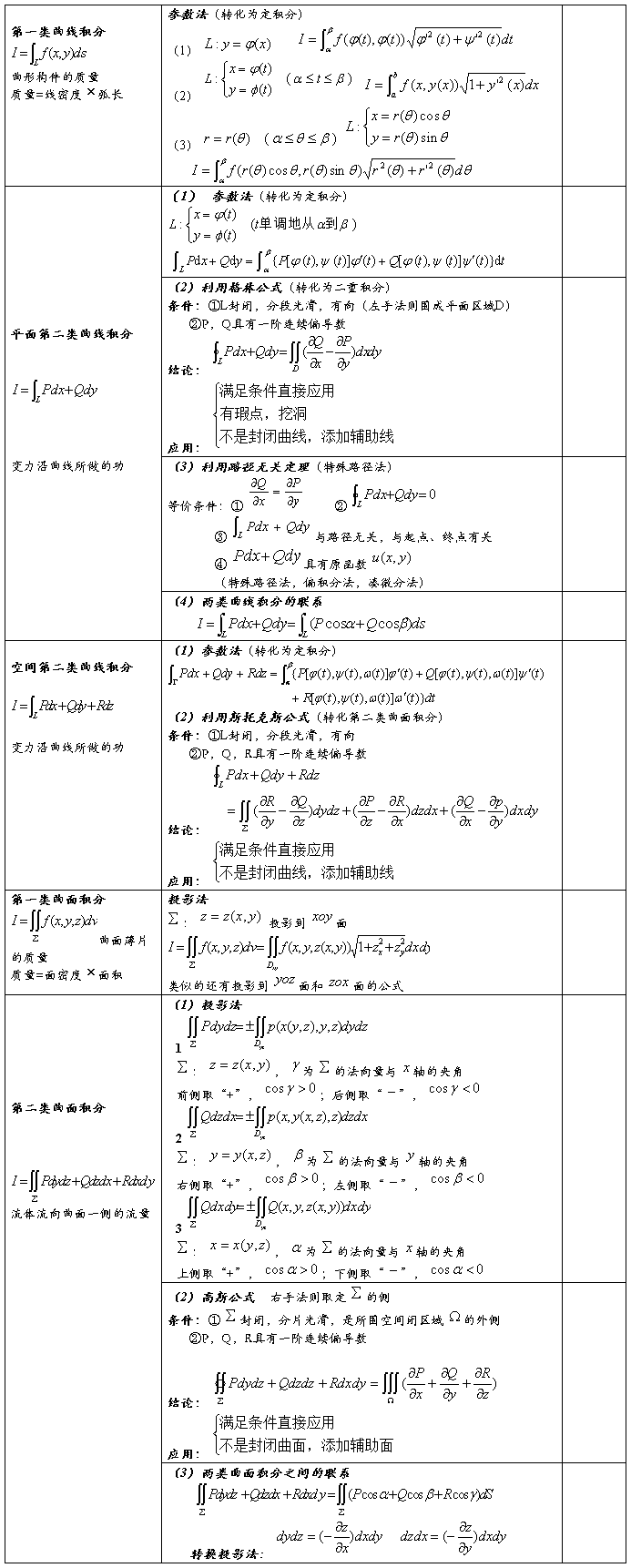
1、二重积分
1.1 X型区域上二重积分(必须的基本方法)
(1)后x先y积分,D往x轴上的投影得区间[a,b];
(2)"x [a,b],X=x截D得截线y1(x)#yy2(x)(小y边界y=y1(x)大y边界y=y2(x));
(3)by(x)蝌f(x,y)dxdy=蝌dx2f(x,y)dyay
D1(x)
1.2 Y型区域上二重积分(必须的基本方法)
(1)后y先x积分,D往y轴上的投影得区间[c,d];
(2)"y [c,d],Y=y截D得截线x1(y)#xx2(y)(小x边界x=x1(y)大x边界x=x2(y));
(3)dx蝌f(x,y)dxdy=蝌dy2(y)f(x,y)dxcx
D1(y)
1.2 极坐标二重积分(为简单的方法)
(1)总是后q先r积分;
(2)br蝌f(x,y)ds=蝌dq2(q)f(rcosq,rsinq)rdr
ar(q)
D1
其中,在D上a是最小的q,b是最大的q;"q [a,b],射线Q=q截D得截线r1(q)#rr2(q)(小r边界r=r1(q)大r边界r=r2(q))。用坐标关系x=rcosq,y=rsinq和面积元素ds=dxdy=rdqdr代入(多一个因子r)。
当积分区域D的边界有圆弧,或被积函数有x2+y2时,用极坐标计算二重积分特别简单。

离 散

数 学 2、三重积分 2.1 二套一方法(必须的基本方法) (1)几何准备 (i) 将积分区域W投影到xOy面,得投影区域Dxy; (ii) 以Dxy的边界曲线为准线,作一个母线平行于z轴的柱面.柱面将闭区域W的边界曲面分割为上、下两片曲面S2:z=z2(x,y()大z边界);S1:z=z1(x,y()小z边界)("(x,y) Dxy,过(x,y)点平行于z轴的直线截W得截线z1(x,y)#zz2(x,y)); (2)z蝌蝌f(x,y,z)dxdydz=蝌dxdy2(x,y)f(x,y,z)dzz。 WD1(x,y)xy还有两种(W往xOz或yOz面投影)类似的二套一方法(举一反三)。 2.2 一套二方法(为简单的方法) (1)几何准备 (i)把W往z投影得轾犏臌c,d; (ii)任意给定z?轾犏臌c,d,用平面Z=z截W得截面(与z有关)Dz; (2)d蝌蝌f(x,y,z)dxdydz=dzf(x,y,z)dxdy, c蝌WDz还有两种(W往x或y轴投影)类似的一套二方法(举一反三)。 2.3 柱面坐标计算三重积分(为简单的方法) (1)把积分写成二套一zx,y)蝌蝌f(x,y,z)dxdydz=蝌dxdy2(f(x,y,z)dzz,y)WD1(xxy(2)用极坐标计算外层的二重积分 z蝌蝌f(x,y,z)dv=蝌dxdy2(x,y)f(x,y,z)dzzWD1(x,y)xybr2(q)zrcosq,rsinq) =蝌dqrdrf(rcosq,rsinq,z)dzar 2(1(q)z1(rcosq,rsinq)(注意:里层的上下限也要用x=rcosq,y=rsinq代入)。(当用极坐标计算外层二重积分简单时。)
…… …… 余下全文
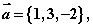
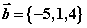 ,则
,则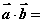 .
.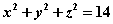 在点
在点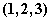 处的法线方程为
处的法线方程为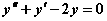 的通解为 .
的通解为 .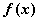 是以
是以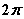 为周期的周期函数,则其傅里叶级数的系数表
为周期的周期函数,则其傅里叶级数的系数表
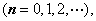
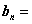
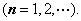
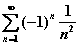 为( ).
为( ).
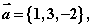
 ,则
,则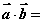
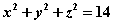 在点
在点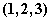 处的法线方程为
处的法线方程为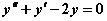 的通解为
的通解为  是以
是以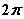 为周期的周期函数,则其傅里叶级数的系数表达式为
为周期的周期函数,则其傅里叶级数的系数表达式为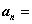
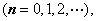
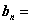
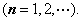
 为( ).
为( ).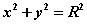 与
与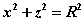
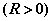 所围成的空间立体的体积为
所围成的空间立体的体积为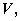 若该立体在第一卦限部分的体积是
若该立体在第一卦限部分的体积是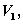 则( ).
则( ).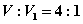 (B)
(B) 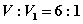 (C)
(C)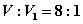 (D)
(D) 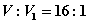
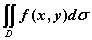 在极坐标系下的面积元素为( ).
在极坐标系下的面积元素为( ).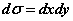 (B)
(B)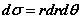 (C)
(C) (D)
(D)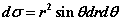
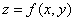 在点
在点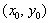 处取得极小值,,则下列结论中正确的是( ).
处取得极小值,,则下列结论中正确的是( ). 在
在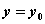 处的导数大于零 (B)
处的导数大于零 (B)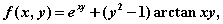 求
求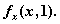
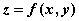 由方程
由方程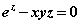 所确定,求
所确定,求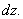
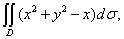 其中
其中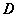 是由直线
是由直线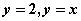 及
及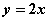 所围成的闭区域.
所围成的闭区域.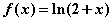 展开为麦克劳林级数.
展开为麦克劳林级数.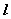 的直角三角形中,求有最大周长的直角三角形.
的直角三角形中,求有最大周长的直角三角形.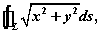 其中
其中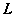 为
为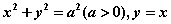 及
及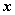 轴在第一象限内所围成的扇形的整个边界.
轴在第一象限内所围成的扇形的整个边界.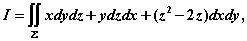 其中
其中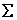 为锥面
为锥面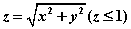 的下侧.
的下侧.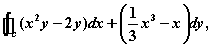 其中
其中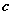 是由直线
是由直线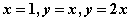 所围成的三角形的正向边界.
所围成的三角形的正向边界.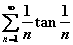 的敛散性.
的敛散性.

 的通解
的通解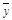 为:
为:
 的特解
的特解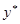 的形式为:
的形式为:
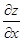 时,应将
时,应将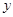 看作常量,对
看作常量,对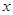 求导,在求
求导,在求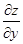 时,应将
时,应将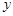 求导,所运用的是一元函数的求导法则与求导公式.
求导,所运用的是一元函数的求导法则与求导公式.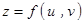 ,
,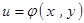 ,
,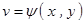 ,则
,则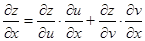 ,
,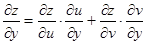
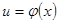 ,
,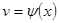 ,则
,则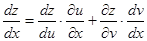
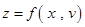 ,
,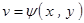 ,则
,则 ,
,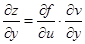
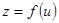 ,
,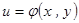 则
则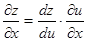 ,
,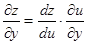
 是由方程
是由方程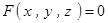 唯一确定的隐函数,则
唯一确定的隐函数,则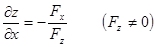 ,
, 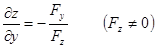
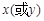 求导解出
求导解出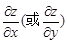 .
.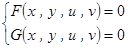 两边同时对
两边同时对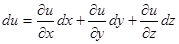
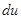 即可.其中要注意应用微分形式的不变性:
即可.其中要注意应用微分形式的不变性: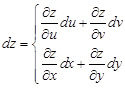


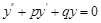 的通解
的通解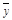 为:
为:
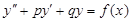 的特解
的特解 的形式为:
的形式为:
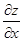 时,应将
时,应将 看作常量,对
看作常量,对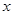 求导,在求
求导,在求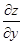 时,应将
时,应将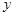 求导,所运用的是一元函数的求导法则与求导公式.
求导,所运用的是一元函数的求导法则与求导公式.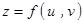 ,
,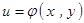 ,
,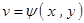 ,则
,则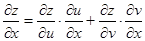 ,
,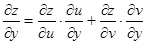
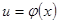 ,
,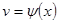 ,则
,则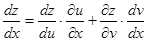
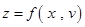 ,
, ,则
,则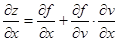 ,
,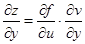
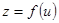 ,
,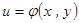 则
则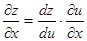 ,
,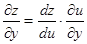
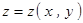 是由方程
是由方程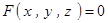 唯一确定的隐函数,则
唯一确定的隐函数,则 ,
, 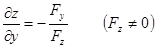
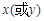 求导解出
求导解出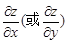 .
.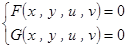 两边同时对
两边同时对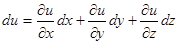
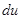 即可.其中要注意应用微分形式的不变性:
即可.其中要注意应用微分形式的不变性:




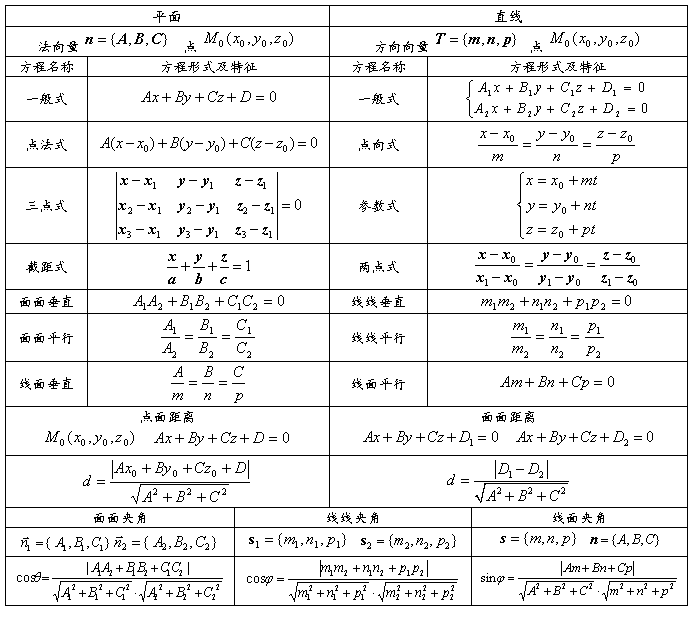





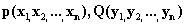 的距离
的距离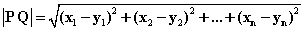
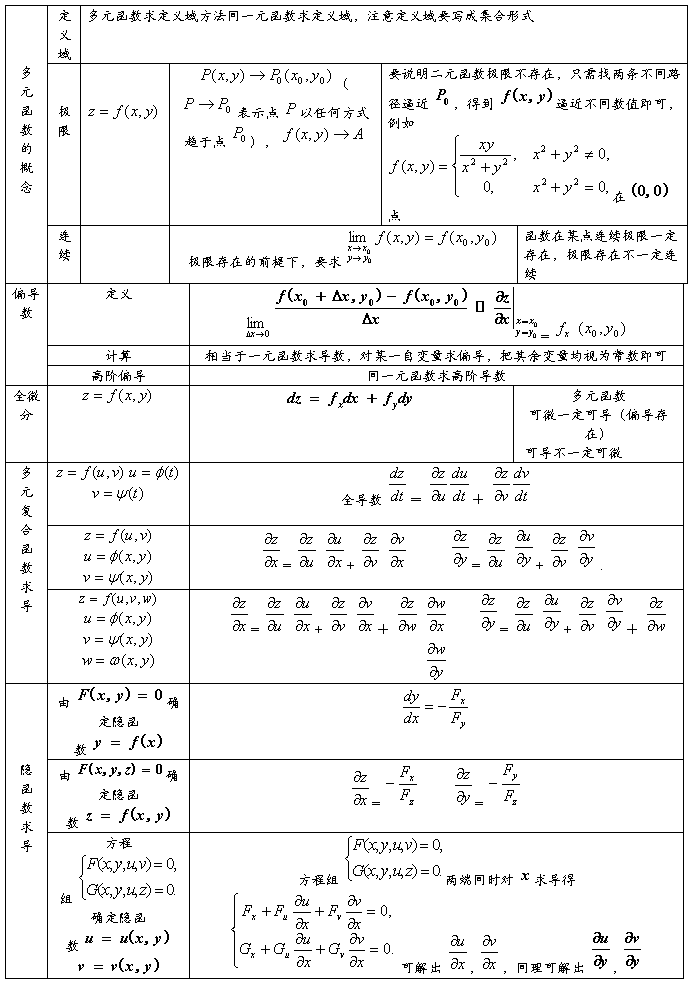
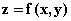 求偏导时,对谁求偏导,就意味着其它的变量都暂时看作常量。比如,
求偏导时,对谁求偏导,就意味着其它的变量都暂时看作常量。比如, 表示对x求偏导,计算时把y 当作常量,只对x求导就可以了。
表示对x求偏导,计算时把y 当作常量,只对x求导就可以了。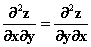 。
。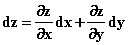 。
。 ,其导数公式:
,其导数公式: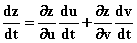 。
。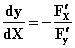 ,其中
,其中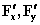 分别表示对x,y求偏导数。
分别表示对x,y求偏导数。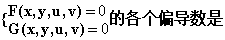 :
: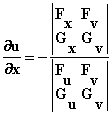 ,
,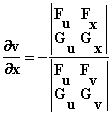 ,
,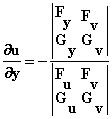 ,
,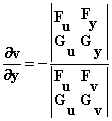 。
。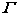 的参数方程是:
的参数方程是: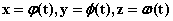 ,则该曲线过点
,则该曲线过点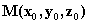 的法平面方程是:
的法平面方程是: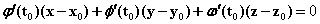
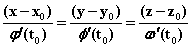 。
。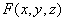 =0在点
=0在点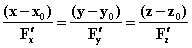 ,
,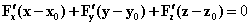 。
。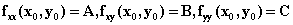
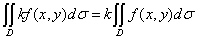

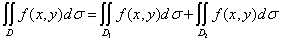
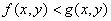 ,则
,则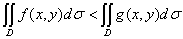
 ,其中s为积分区域D的面积
,其中s为积分区域D的面积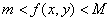 ,则
,则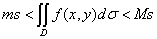
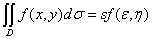 ,其中
,其中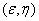 是区域D中的点
是区域D中的点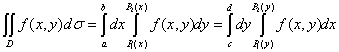 ,有的积分可以随意选择积分次序,但是做题的复杂性会出现不同,这时选择积分次序就比较重要,主要依据通过积分区域和被积函数来确定
,有的积分可以随意选择积分次序,但是做题的复杂性会出现不同,这时选择积分次序就比较重要,主要依据通过积分区域和被积函数来确定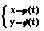 ,
,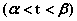 ,则
,则
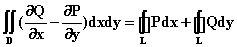
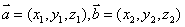 ,则有
,则有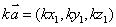 ,
, 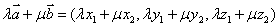 ,若
,若 ,则
,则