圆锥曲线总结
椭 圆
典例精析
题型一 求椭圆的标准方程
45【例1】已知点P在以坐标轴为对称轴的椭圆上,点P和 3
25,过P作长轴的垂线恰好过椭圆的一个焦点,求椭圆的方程. 3
题型二 椭圆的几何性质的运用
【例2】已知F1、F2是椭圆的两个焦点,P为椭圆上一点,∠F1PF2=60°.
(1)求椭圆离心率的范围;
(2)求证:△F1PF2的面积只与椭圆的短轴长有关.
题型三 有关椭圆与直线综合问题
x2y2
【例3】【20xx高考浙江理21】如图,椭圆C:2+2?1(a>b>0)的离心ab
1率为,其左焦点到点P(2,
1)O的直线l与C相2
交于A,B两点,且线段AB被直线OP平分.
(Ⅰ)求椭圆C的方程;
(Ⅱ) 求?ABP的面积取最大时直线l的方程.
.
例4.【20xx高考广东理20】 x2y2在平面直角坐标系xOy中,已知椭圆C1:2?2?1(a?b?
0)的离心率e=,且椭圆C上的点到Q(0,ab3
2)的距离的最大值为3.
(1)求椭圆C的方程;
(2)在椭圆C上,是否存在点M(m,n)使得直线l:mx+ny=1与圆O:x2+y2=1相交于不同的两点A、B,且△OAB的面积最大?若存在,求出点M的坐标及相对应的△
OAB的面积;若不存在,请说明理由.
同步练习
x2
?y2?1的右焦点为F,右准线为l,点A?l,线段AF交C于点B,若1(20xx全国卷Ⅰ理)已知椭圆C:2
FA?3FB,则|AF|=( )
x2y2
.2(20xx浙江文)已知椭圆2?2?1(a?b?0)的左焦点为F,右顶点为A,点B在椭圆上,且BF?x轴,ab
直线AB交y轴于点P.若AP?2PB,则椭圆的离心率是( )
A
11 B
. C. D.322
…… …… 余下全文

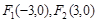 ,在满足下列条件的平面上动点P的轨迹中,是椭圆的是( )
,在满足下列条件的平面上动点P的轨迹中,是椭圆的是( ) 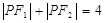 B.
B.
 D.
D.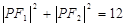
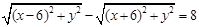 表示的曲线是_____
表示的曲线是_____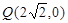 及抛物线
及抛物线 上一动点P(x,y),则y+|PQ|的最小值是___
上一动点P(x,y),则y+|PQ|的最小值是___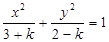 表示椭圆,则
表示椭圆,则 的取值范围为____;
的取值范围为____;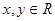 ,且
,且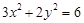 ,则
,则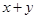 的最大值是___,
的最大值是___,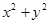 的最小值是
的最小值是 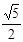 ,且与椭圆
,且与椭圆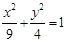 有公共焦点,则该双曲线的方程_______;
有公共焦点,则该双曲线的方程_______;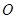 ,焦点
,焦点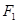 、
、 在坐标轴上,离心率
在坐标轴上,离心率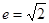 的双曲线C过点
的双曲线C过点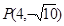 ,则C的方程为
,则C的方程为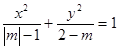 表示焦点在y轴上的椭圆,则m的取值范围是( )
表示焦点在y轴上的椭圆,则m的取值范围是( )  的离心率
的离心率 ,则
,则 的值是__
的值是__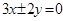 ,则该双曲线的离心率等于______
,则该双曲线的离心率等于______ 的离心率为
的离心率为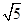 ,则
,则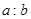 =
= 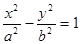 (a>0,b>0)中,离心率e∈[
(a>0,b>0)中,离心率e∈[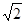 ,2],则两条渐近线夹角θ的取值范围是____
,2],则两条渐近线夹角θ的取值范围是____ 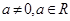 ,则抛物线
,则抛物线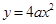 的焦点坐标为________
的焦点坐标为________ )、B(
)、B( )两点,则弦长|AB|为:
)两点,则弦长|AB|为:
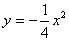 的焦点作倾斜角为
的焦点作倾斜角为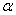 的直线
的直线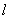 与抛物线交于A、B两点,旦|AB|=8,求倾斜角
与抛物线交于A、B两点,旦|AB|=8,求倾斜角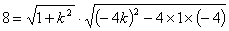 ∴
∴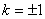
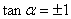 得:
得: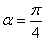 或
或 .
.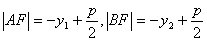
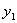 +y2)+p=-[(kx1-1)+(kx2-1)]+p=-k(
+y2)+p=-[(kx1-1)+(kx2-1)]+p=-k(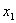 +x2)+2+p.由上述解法易求得结果,可由同学们自己试试完成.
+x2)+2+p.由上述解法易求得结果,可由同学们自己试试完成.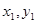 )、B(
)、B(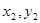 )两点,则弦长|AB|为:
)两点,则弦长|AB|为: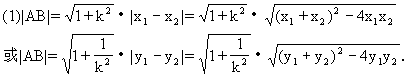
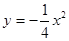 的焦点作倾斜角为
的焦点作倾斜角为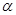 的直线
的直线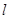 与抛物线交于A、B两点,旦|AB|=8,求倾斜角
与抛物线交于A、B两点,旦|AB|=8,求倾斜角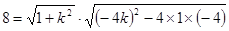 ∴
∴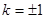
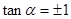 得:
得: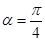 或
或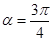 .
.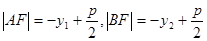
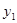 +y2)+p=-[(kx1-1)+(kx2-1)]+p=-k(
+y2)+p=-[(kx1-1)+(kx2-1)]+p=-k( +x2)+2+p.由上述解法易求得结果,可由同学们自己试试完成.
+x2)+2+p.由上述解法易求得结果,可由同学们自己试试完成. )、B(
)、B(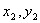 )两点,则弦长|AB|为:
)两点,则弦长|AB|为: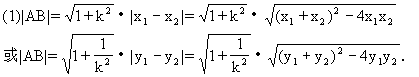
 的焦点作倾斜角为
的焦点作倾斜角为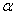 的直线
的直线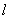 与抛物线交于A、B两点,旦|AB|=8,求倾斜角
与抛物线交于A、B两点,旦|AB|=8,求倾斜角 ∴
∴
 得:
得: 或
或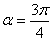 .
.
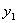 +y2)+p=-[(kx1-1)+(kx2-1)]+p=-k(
+y2)+p=-[(kx1-1)+(kx2-1)]+p=-k( +x2)+2+p.由上述解法易求得结果,可由同学们自己试试完成.
+x2)+2+p.由上述解法易求得结果,可由同学们自己试试完成. 、
、 、
、 、
、 、
、 、渐近线。
、渐近线。 、
、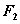 分别为双曲线
分别为双曲线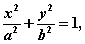 (
(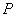 ,满足
,满足 ,且
,且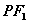 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )