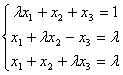线性代数知识点总结
第一章 行列式
(一)要点
1、二阶、三阶行列式
2、全排列和逆序数,奇偶排列(可以不介绍对换及有关定理),n阶行列式的定义
3、行列式的性质
4、n阶行列式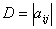 ,元素
,元素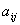 的余子式和代数余子式,行列式按行(列)展开定理
的余子式和代数余子式,行列式按行(列)展开定理
5、克莱姆法则
(二)基本要求
1、理解n阶行列式的定义
2、掌握n阶行列式的性质
3、会用定义判定行列式中项的符号
4、理解和掌握行列式按行(列)展开的计算方法,即
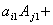
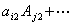
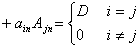
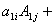

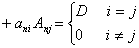
5、会用行列式的性质简化行列式的计算,并掌握几个基本方法:
归化为上三角或下三角行列式,
各行(列)元素之和等于同一个常数的行列式,
利用展开式计算
6、掌握应用克莱姆法则的条件及结论
会用克莱姆法则解低阶的线性方程组
7、了解 个方程
个方程 个未知量的齐次线性方程组有非零解的充要条件
个未知量的齐次线性方程组有非零解的充要条件
第二章 矩阵
(一)要点
1、矩阵的概念
 矩阵
矩阵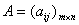 是一个矩阵表。当
是一个矩阵表。当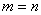 时,称
时,称 为
为 阶矩阵,此时由
阶矩阵,此时由 的元素按原来排列的形式构成的
的元素按原来排列的形式构成的 阶行列式,称为矩阵
阶行列式,称为矩阵 的行列式,记为
的行列式,记为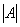 .
.
注:矩阵和行列式是两个完全不同的两个概念。
2、几种特殊的矩阵:对角阵;数量阵;单位阵;三角形矩阵;对称矩阵
3、矩阵的运算;矩阵的加减法;数与矩阵的乘法;矩阵的转置;矩阵的乘法
(1)矩阵的乘法不满足交换律和消去律,两个非零矩阵相乘可能是零矩阵。
如果两矩阵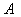 与
与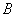 相乘,有
相乘,有 ,则称矩阵
,则称矩阵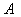 与
与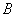 可换。
可换。
…… …… 余下全文


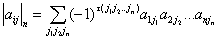
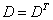 )
)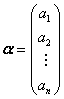 列向量,
列向量,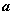 =(
=(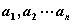 )行向量。
)行向量。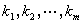 使
使 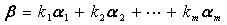
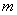 个不全为零的常数
个不全为零的常数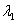 ,
, ,
,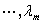 使满足
使满足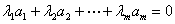 (3-4)
(3-4)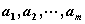 是线性相关的,否则,便称则
是线性相关的,否则,便称则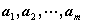 ,讨论其相关性的方法是:
,讨论其相关性的方法是: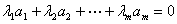 ,求出
,求出 ,
,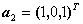 ,
, 的线性相关性
的线性相关性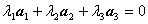
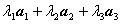 =
=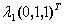 +
+ +
+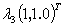
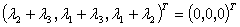
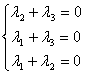 由此推得
由此推得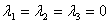 ,这表明只有
,这表明只有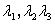 全为零才使
全为零才使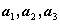 线性无关。
线性无关。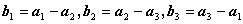 讨论向量
讨论向量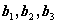 的线性相关性
的线性相关性

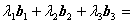
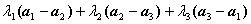
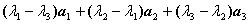

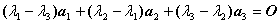
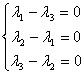 由此解得
由此解得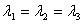 。
。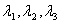 有无穷多组,不妨取
有无穷多组,不妨取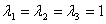 ,这三个不全为零的数,它使
,这三个不全为零的数,它使 
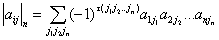
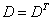 )
) 的逆矩阵为 .
的逆矩阵为 .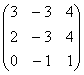
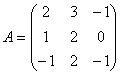 ,
,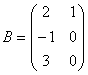 , 求
, 求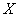 使
使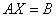 .
. 矩阵
矩阵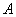 ,且
,且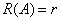 ,
,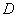 为
为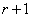 阶子式,则
阶子式,则 _______.
_______.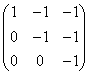 的秩等于__________.
的秩等于__________.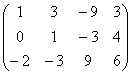
 有非零解的充要条件是_____.
有非零解的充要条件是_____.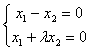 有非零解,则
有非零解,则 .
.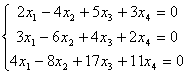
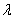 取何值时,下列方程组有唯一解,无解或有无穷多解?并在有无穷多解时求解.
取何值时,下列方程组有唯一解,无解或有无穷多解?并在有无穷多解时求解.