第二章 随机变量及其分布
随机变量:
设随机试验的样本空间为S={e},X=X{e}是定义在样本空间S上的实值单值函数,称X=X{e}为随机变量
一般以大写字母X,Y,Z,W,…表示随机变量,而以小写字母x,y,z,……表示实数
离散型随机变量:
全部可能取到的不相同的值是有限个或可列无限多个的随机变量
?怎么判断可列无限多个呢?
离散型随机变量的分布律:
1)等式形式表示为
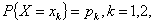 …
…
2)表格形式表示:

三种重要的离散型随机变量:
1.(0-1)分布
设随机变量X只能取0与1两个值,它的分布律是
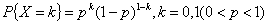
则称X服从(0-1)分布或两点分布
其分布律也可写成:

2.伯努利试验、二项分布
伯努利试验:设试验E只有两个可能结果:A及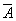 ,则称E为伯努利试验,设P(A)=p(0<p<1),此时P(
,则称E为伯努利试验,设P(A)=p(0<p<1),此时P(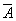 )=1-p。
)=1-p。
将E独立地重复进行n次,则称这一串重复的独立试验为n重伯努利试验
设X为n重伯努利试验中事件A发生的次数,则X是一个随机变量,且满足
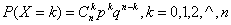 ,
,
称随机变量X服从参数为n,p的二项分布,记为X~b(n,p)
3.泊松分布
设随机变量X所以可能取的值为0,1,2,…,而取各个值的概率为
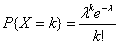 ,k=0,1,2,……
,k=0,1,2,……
其中λ>0是常数,则称X服从参数为λ的泊松分布,记为X~π(λ)
非离散型随机变量:
其可能取值不能一个一个地列举出来
非离散型随机变量取任一指定的实数值的概率都等于0
分布函数:
设X是一个随机变量,x是任意实数,函数F(x)=P{X≤x}称为X的分布函数
对于任意实数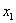 ,
,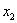 (
(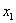 <
<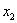 ),有
),有
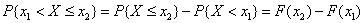
分布函数完整地描述了随机变量的统计规律性。
…… …… 余下全文

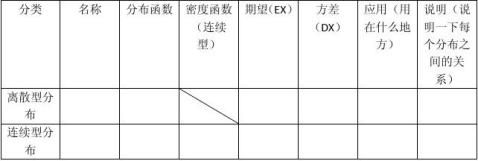
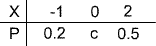

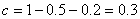
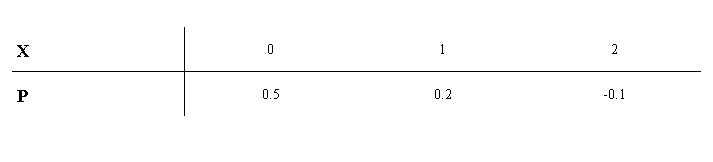
 A. B.
A. B.

 C. D.
C. D.
 (1)事件的包含与相等:
(1)事件的包含与相等: (2)事件的和(或并):
(2)事件的和(或并):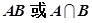 (3)事件的积(或交):
(3)事件的积(或交):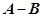 (4)事件的差:
(4)事件的差: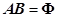 (5)互不相容事件:
(5)互不相容事件: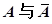 (6)对立事件:
(6)对立事件: (1)
(1) …
…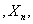 …相互独立(是指对于任意n>1,
…相互独立(是指对于任意n>1,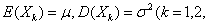 …
…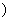 。作前n个随机变量的算术平均
。作前n个随机变量的算术平均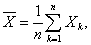
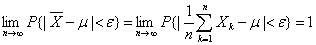
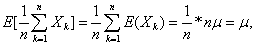
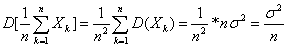 ,
,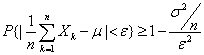
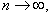 并注意到概率不能大于1,即得
并注意到概率不能大于1,即得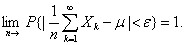
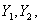 …
…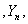 …是一个随机变量序列,a是一个常数。若对于任意正数ε,有
…是一个随机变量序列,a是一个常数。若对于任意正数ε,有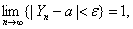

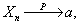
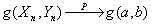
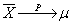
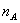 是n次独立重复试验中事件A发生的次数。p是事件A在每次试验中发生的概率,则对于任意正数ε>0,有
是n次独立重复试验中事件A发生的次数。p是事件A在每次试验中发生的概率,则对于任意正数ε>0,有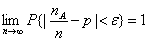 或
或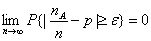
 ,有
,有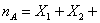 …
…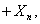
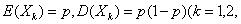 …
…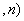 ,由定理一得
,由定理一得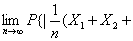 …
…
 …
…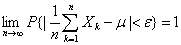
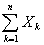 的标准化变量:
的标准化变量: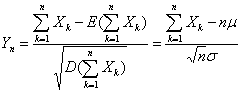
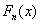 对于任意x满足
对于任意x满足
 均值为μ,方差为
均值为μ,方差为
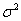 >0的独立同分布的随机变量之和
>0的独立同分布的随机变量之和
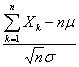 ~
~
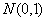
 这样上述结果可写成:
这样上述结果可写成:

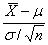 ~
~
 ~
~
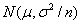
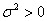 的独立同分布的随机变量
的独立同分布的随机变量 ,当n充分大时近似地服从均值为μ,方差为
,当n充分大时近似地服从均值为μ,方差为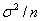 的正态分布
的正态分布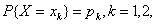 …
…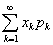 绝对收敛,则称级数
绝对收敛,则称级数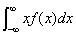 绝对收敛,则称积分
绝对收敛,则称积分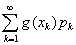 绝对收敛,则有
绝对收敛,则有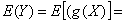
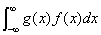 绝对收敛,则有E(Y)=E[g(X)]=
绝对收敛,则有E(Y)=E[g(X)]= 存在,则称
存在,则称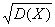 ,记为σ(X),称为标准差或均方差
,记为σ(X),称为标准差或均方差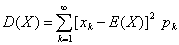
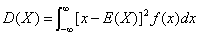
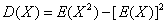
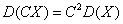
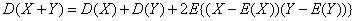
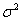 ,则对于任意正数
,则对于任意正数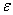 ,不等式
,不等式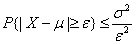 成立
成立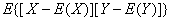 称为随机变量X与Y的协方差,记为Cov(X,Y),即
称为随机变量X与Y的协方差,记为Cov(X,Y),即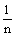 ,如果某个事件A包含的结果有m个,那么事件A的概率
,如果某个事件A包含的结果有m个,那么事件A的概率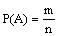 .
.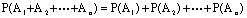 .
. ②对立事件:两个事件必有一个发生的互斥事件叫对立事件. 例如:从1~52张扑克牌中任取一张抽到“红桃”与抽到“黑桃”互为互斥事件,因为其中一个不可能同时发生,但又不能保证其中一个必然发生,故不是对立事件.而抽到“红色牌”与抽到黑色牌“互为对立事件,因为其中一个必发生.
②对立事件:两个事件必有一个发生的互斥事件叫对立事件. 例如:从1~52张扑克牌中任取一张抽到“红桃”与抽到“黑桃”互为互斥事件,因为其中一个不可能同时发生,但又不能保证其中一个必然发生,故不是对立事件.而抽到“红色牌”与抽到黑色牌“互为对立事件,因为其中一个必发生.