总结求逆矩阵方法

根据矩阵特点用不用的分解，写成几个例程，每次实验之前进行尝试，根据尝试结果在算法里决定里决定用哪个。

问：
1.全阶矩阵A的求逆运算inv(A) 和稀疏矩阵B（阶数和a一样）
的求逆运算inv(B)是不是采取一样的方法啊？也就是说他们的
计算量是不是一样的啊？不会因为是稀疏矩阵就采取特殊的
方法来处理求逆吧？
我电脑内存256M ，做4096*4096的矩阵求逆还可以，上万阶的
就跑不动了
稀疏存储方式会减少不必要的计算，虽然原理还是一样，不过
计算量大大减少了。
      
2.如果一个矩阵C非零元素都集中在主对角线的周围，那么对C求逆最好
应该采用什么样的方法最好呢？
一般还是用LU分解＋前后迭代的方法，如果矩阵对角占优就更好办了。
只不过还是需要稀疏存储。

稀疏矩阵的逆一般不会是稀疏矩阵，所以对高阶的稀疏矩阵求逆，
是不可行的，对1万阶的全矩阵需要的内存差不多已经达到了pc的
极限，我想最好的办法就是迭代，既然是稀疏，乘法的次数就有限，
效率还是很高的。

不过求逆运算基本上就是解方程，对稀疏矩阵，特别是他那种基本上非零元素都在对角线附近的矩阵来说，LU分解不会产生很多的注入元，所以用LU分解解方程方法的方法是可行的。
如果用迭代法，好像也就是共轭梯度法了。

C的资源网络上有很多 google一下
或者到www.csdn.net，oonumerics.org上找找
或者用IMSL for C
或者用Lapack
或者用Matlab+C混合编程
有现成代码，但要你自己找了
也可以使用程序库


second
30,000*30,000的稀疏矩阵求逆如何实现？
试试基于krylov子空间方法的算法吧。
如arnoldi和GMRES方法。

matlab中有函数可以直接调用。
直接help gmres就可以了。

如果效果还不好 。
就用用预处理技术。
比如不完全lu预处理方法。。等等。。
各种各样的预处理+GMRES是现在解决大规模稀疏矩阵的主力方法。。
维数再多还是用不完全LU分解预处理+CG or Gmres
我一个同学这么求过200W阶的矩阵
求逆一般是不可取的，无需多说。但稀疏矩阵的直接解法还是不少的。基本上都是对矩阵进行重新排序以期减少填充或运算量。
在matlab里面，有许多算法可以利用：
colamd, colmmd, colperm, spparms, symamd, symmmd, symrcm.
根据是否对称，采用LU分解或者chol分解。
这些算法在internet上搜一下，很多都有相应的C或fortran版本。

稀疏矩阵的存储最常见的是压缩列（行）存储，最近发现一种利用hash表来存储的，其存取复杂度是O（1）,很是不错。有幸趣的可以看看下面网页咯，作者提供了源程序。

事实上Hash表存储的效率也跟Hash算法有关，弄不好的话，不见得比直接按行或者列
顺序检索快。而且规模越大，效率肯定越来越低。

http://www.informatik.hs-bremen.de/~brey/

对称正定的稀疏矩阵很好办啊，用LU分解就可以了。

如果维数实在太大，比如超过10^4量级，那就只能用
共轭梯度法之类的迭代法求解了。
好多文献中用Cholesky分解处理的，好像结果还可以
你觉得LL’分解不会破坏矩阵的稀疏性么——如果矩阵不是带状的话？
而且数值稳定性也有问题。
对于一些注入元不是很多的矩阵这应该是个好办法。
但是对于有些矩阵，LU分解后可能就把整个矩阵充满了。~
这是比较郁闷的事情。。

third
带状矩阵的逆有快速算法吗？
我觉得这个说法不对，至少在Matlab里面，使用稀疏矩阵求逆对于效率的提高还是很显著的。利用稀疏特性，很多对于零元素的操作就省掉了。如果原矩阵还是对称的，可以考虑三角分解，把单位阵的列向量作为右端项，求解得到的是对应的逆阵的列向量。
但是，按照前辈的说法，“绝大部分情况下，求逆阵肯定不是必需的”，这一说法我现在还是挺赞同的。 至少， 一般我们不会在有限元求解或者普通的线性方程组求解的时候，是先对系数矩阵求逆的吧。 所以，我认为，逆阵在数学上很漂亮，对于公式推导有所帮助，但是在数值计算中是应该尽量避免直接计算它的，而且，更重要的是，在绝大部分情况下，是可以避免的。

…… …… 余下全文

总结求逆矩阵方法 直接算会死人的。根据矩阵特点用不用的分解，写成几个例程，每次实验之前进行尝试，根据尝试结果在算法里决定里决定用哪个。

irst

我想问：

1.全阶矩阵A的求逆运算inv(A) 和稀疏矩阵B（阶数和a一样）

的求逆运算inv(B)是不是采取一样的方法啊？也就是说他们的

计算量是不是一样的啊？不会因为是稀疏矩阵就采取特殊的 方法来处理求逆吧？

我电脑内存256M ，做4096*4096的矩阵求逆还可以，上万阶的 就跑不动了

稀疏存储方式会减少不必要的计算，虽然原理还是一样，不过

计算量大大减少了。

2.如果一个矩阵C非零元素都集中在主对角线的周围，那么对C求逆最好 应该采用什么样的方法最好呢？

一般还是用LU分解＋前后迭代的方法，如果矩阵对角占优就更好办了。 只不过还是需要稀疏存储。

稀疏矩阵的逆一般不会是稀疏矩阵，所以对高阶的稀疏矩阵求逆， 是不可行的，对1万阶的全矩阵需要的内存差不多已经达到了pc的 极限，我想最好的办法就是迭代，既然是稀疏，乘法的次数就有限， 效率还是很高的。

不过求逆运算基本上就是解方程，对稀疏矩阵，特别是他那种基本上非零元素都在对角线附近的矩阵来说，LU分解不会产生很多的注入元，所以用LU分解解方程方法的方法是可行的。

如果用迭代法，好像也就是共轭梯度法了。

C的资源网络上有很多 google一下 或者到，oonumerics.org上找找

或者用IMSL for C

或者用Lapack

或者用Matlab+C混合编程

有现成代码，但要你自己找了

也可以使用程序库

second

30,000*30,000的稀疏矩阵求逆如何实现？ 试试基于krylov子空间方法的算法吧。

如arnoldi和GMRES方法。

matlab中有函数可以直接调用。

直接help gmres就可以了。

…… …… 余下全文

求逆矩阵的方法与矩阵的秩

    一、矩阵的初等行变换

    定义2.13   矩阵的初等行变换是指对矩阵进行下列三种变换：

    (1)  将矩阵中某两行对换位置；

    (2)  将某一行遍乘一个非零常数k；

    (3)  将矩阵的某一行遍乘一个常数k加至另一行.

并称(1)为对换变换，称(2)为倍乘变换，称(3)为倍加变换.

    矩阵A经过初等行变换后变为B，用

A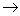B

表示，并称矩阵B与A是等价的.

    （下面我们把）第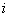行和第j行的对换变换，简记为“   ，  ”；把第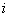行遍乘k倍的倍乘变换，简记为“  k”；第j行的k倍加至第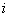行上的倍加变换，简记为“   +   k”.

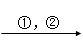    例如，矩阵  A =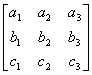             

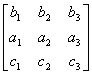
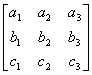
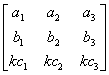
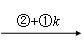
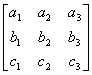
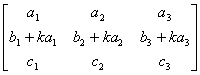
…… …… 余下全文

伴随矩阵相关问题求解方法小结（2）

来源：文都教育

在一部分求矩阵的行列式的题目中，会将其与伴随矩阵相结合进行考查. 根据性质AA*?A*A?AE，很容易得到伴随矩阵的行列式，即

若A为n阶矩阵，则A?A*n?1.

*?1例1 设A，B为n阶矩阵，A?2，B??3，则2AB?.

解 由kA?knA，A*?AA?1，A?A*n?1?1及B?B，得到

2A*B?1?2A*B?1?2nA*?B)?2nAn?1B??22n?1.

伴随矩阵的每个元素都是原矩阵A的代数余子式，使得伴随矩阵与矩阵A之间有各种联系. 与伴随矩阵相关的另一个重要的知识点是求矩阵的秩. 矩阵A的秩与其伴随矩阵A的秩之间有如下关系： *

?n,r(A)?n,?设A为n（n?2）阶方阵, 则r(A*)??1,r(A)?n?1, r(A)表示秩(A).

?0,r(A)?n?1.?

上述关系在解与伴随矩阵相关的求解矩阵的秩的题目应用广泛，不仅要会求已知矩阵A的秩求矩阵A*的秩，还要会求已知矩阵A*的秩求矩阵A的秩，应该在理解的基础上熟记，遇到同类题目可直接应用，将会对解题提供很大的便利.

例2 设四阶方阵A的秩为2，则其伴随矩阵A的秩为.

解 根据上述矩阵A的秩与其伴随矩阵A的秩之间的关系，因为A的秩为2<4，因此可得矩阵A的秩为0.

例3 设A是n阶可逆矩阵，A是A的伴随矩阵，常数k≠0，则(kA)等于（ ）. *****?1

?1?1A. kAA B. kA?1A C. k?1A?1A?1 D. kA?1A?1

解 因为A可逆，所以A*?AA?1，从而

(kA*)?1?k?1(A*)?1

?k?1(AA?1)?1

?k?1A(A?1)?1

?k?1A?1?1A. 故选择B.

综上可知，掌握与伴随矩阵相关问题的求解方法，可以很好地解决诸如求已知矩阵A求其伴随矩阵或已知其伴随矩阵求矩阵A，求与伴随矩阵有关的秩，及求逆矩阵问题. 在《2016考研数学客观题简化求解》赠送的《客观题同步测试题》中会有相对于的测试题，帮助考生巩固复习效果，是考生复习过程中的得力助手.

…… …… 余下全文

一，求极限的方法横向总结：

1带根式的分式或简单根式加减法求极限：1）根式相加减或只有分子带根式：用平方差公式，凑平方（有分式又同时出现未知数的不同次幂：将未知数全部化到分子或分母的位置上）

2）分子分母都带根式：将分母分子同时乘以不同的对应分式凑成完全平方式（常用到

2分子分母都是有界变量与无穷大量加和求极限：分子与分母同时除以该无穷大量凑出无穷小量与有界变量的乘积结果还是无穷小量。

3等差数列与等比数列和求极限：用求和公式。

4分母是乘积分子是相同常数的n项的和求极限：列项求和

5分子分母都是未知数的不同次幂求极限：看未知数的幂数，分子大为无穷大，分子小为无穷小或须先通分。

6运用重要极限求极限（基本）。

7乘除法中用等价无穷小量求极限。

8函数在一点处连续时，函数的极限等于极限的函数。

9常数比0型求极限：先求倒数的极限。

10根号套根号型：约分，注意别约错了。

11三角函数的加减求极限：用三角函数公式，将sin化cos

二，求极限的方法纵向总结：

1未知数趋近于一个常数求极限：分子分母凑出（x-常数）的形式，然后约分（因为x不等于该常数所以可以约分）最后将该常数带入其他式子。

2未知数趋近于0或无穷：1）将x放在相同的位置

2）用无穷小量与有界变量的乘积

3）2个重要极限

4）分式解法（上述）

…… …… 余下全文

部分规律小结

1 带根式的分式或简单根式加减法求极限：

a根式相加减或只有分子带根式：用平方差公式，凑平方（有分式又同时出现未知数的不同次幂∶将未知数全部化到分子或分母的位置上）

b分子分母都带根式：将分母分子同时乘以不同的对应分式凑成完全平方式 2 分子分母都是有界变量与无穷大量加和求极限：分子与分母同时除以该无穷大量凑出无穷小量与有界变量的乘积结果还是无穷小量。

3 等差数列与等比数列和求极限：用求和公式。

4 分母是乘积分子是相同常数的 n 项的和求极限：列项求和。

5 分子分母都是未知数的不同次幂求极限：看未知数的幂数，分子大为无穷大，分子小为无穷小或须先通分。

6 运用重要极限求极限（基本）。

7 乘除法中用等价无穷小量求极限。

8 函数在一点处连续时，函数的极限等于极限的函数。

9 常数比 0 型求极限：先求倒数的极限。

10 根号套根号型：约分，注意别约错了。

11 三角函数的加减求极限：用三角函数公式，将 sin 化 cos 。

…… …… 余下全文

数列求和的基本方法和技巧

数列求和是数列的重要内容之一，除了等差数列和等比数列有求和公式外，大部分数列的求和都需要一定的技巧.

一、利用常用求和公式求和

   利用下列常用求和公式求和是数列求和的最基本最重要的方法.

1、 等差数列求和公式：  

2、等比数列求和公式：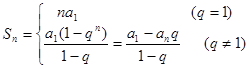                

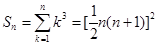3、（要记忆）    4、（要记忆）

[例1] 已知，求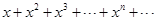的前n项和.

解：由

 由等比数列求和公式得 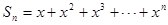                     （利用常用公式）

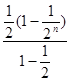                       ＝＝＝1－

二、错位相减法求和

这种方法是在推导等比数列的前n项和公式时所用的方法，这种方法主要用于求数列{a_n·　b_n}的前n项和，其中{ a_n }、{ b_n }分别是等差数列和等比数列.

[例2] 求和：………………………①

解：由题可知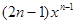，{}的通项是等差数列{2n－1}的通项与等比数列{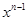}的通项之积

设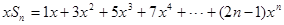………………………. ②    （设制错位）

…… …… 余下全文