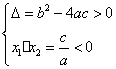二次函数
一、 函数定义与表达式
1. 一般式: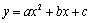 (
(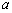 ,
,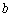 ,
,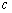 为常数,
为常数,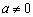 );
);
2. 顶点式: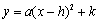 (
(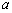 ,
,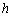 ,
,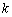 为常数,
为常数,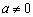 );
);
 3. 交点式:
3. 交点式: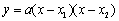 (
(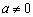 ,
,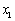 ,
, 是抛物线与
是抛物线与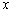 轴两交点的横坐标).
轴两交点的横坐标).

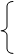 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与
注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与
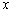 轴有交点,即
轴有交点,即
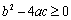 时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化
时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化
二、 函数图像的性质——抛物线
(1)开口方向——二次项系数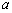
二次函数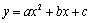 中,
中,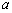 作为二次项系数,显然
作为二次项系数,显然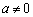 .
.
当 时,抛物线开口向上,
时,抛物线开口向上,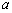 的值越大,开口越小,反之
的值越大,开口越小,反之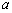 的值越小,开口越大;
的值越小,开口越大;
当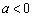 时,抛物线开口向下,
时,抛物线开口向下,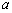 的值越小,开口越小,反之
的值越小,开口越小,反之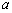 的值越大,开口越大.
的值越大,开口越大.
总结起来,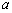 决定了抛物线开口的大小和方向,
决定了抛物线开口的大小和方向,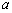 的正负决定开口方向,
的正负决定开口方向,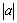 的大小决定开口的大小.IaI越大开口就越小,IaI越小开口就越大.
的大小决定开口的大小.IaI越大开口就越小,IaI越小开口就越大.


(2)抛物线是轴对称图形,对称轴为直线
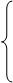 一般式:
一般式: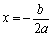
对称轴 顶点式:x=h
两根式:x=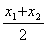
(3)对称轴位置
一次项系数b和二次项系数a共同决定对称轴的位置。(“左同右异”)
 a与b同号(即ab>0) 对称轴在y轴左侧
a与b同号(即ab>0) 对称轴在y轴左侧
 a与b异号(即ab<0) 对称轴在y轴右侧
a与b异号(即ab<0) 对称轴在y轴右侧
…… …… 余下全文

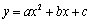 (
(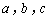 是常数,
是常数, )的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数
)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数 可以为零.二次函数的定义域是全体实数.
可以为零.二次函数的定义域是全体实数.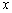 的二次式,
的二次式, 是二次项系数,
是二次项系数,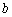 是一次项系数,
是一次项系数,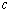 是常数项.
是常数项. 的性质:
的性质:
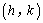 ;
;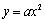 的形状不变,将其顶点平移到
的形状不变,将其顶点平移到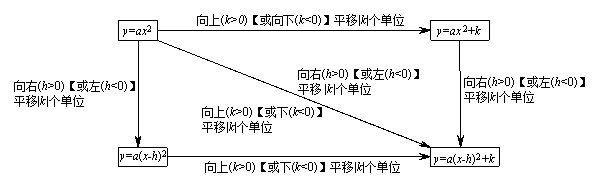
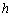 值正右移,负左移;
值正右移,负左移;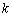 值正上移,负下移”.
值正上移,负下移”.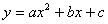 沿
沿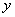 轴平移:向上(下)平移
轴平移:向上(下)平移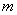 个单位,
个单位, (或
(或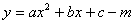 )
)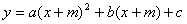 (或
(或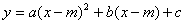 )
)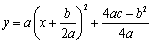 ,其中
,其中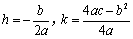 .
.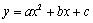 图象的画法
图象的画法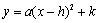 ,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与
,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与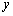 轴的交点
轴的交点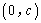 、以及
、以及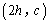 、与
、与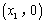 ,
,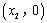 (若与
(若与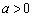 时,抛物线开口向上,对称轴为
时,抛物线开口向上,对称轴为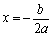 ,顶点坐标为
,顶点坐标为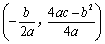 .
.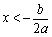 时,
时,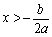 时,
时,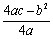 .
.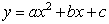 (
( ); ②顶点式:
); ②顶点式: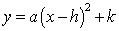 (
(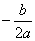 ,
,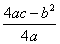 ) ②(
) ②(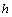 ,
, )
)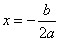 时,
时,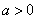 ,
,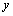 有最小值为
有最小值为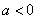 ,
,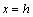 时,
时,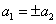 两函数图象大小形状相同.(即
两函数图象大小形状相同.(即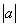 相等的抛物线为全等型抛物线)
相等的抛物线为全等型抛物线)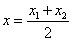 (其中x1、x2为抛物线上对称点的横坐标)
(其中x1、x2为抛物线上对称点的横坐标)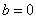 ,对称轴为
,对称轴为 ,即a、b异号,对称轴在
,即a、b异号,对称轴在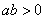 ,即a、b同号,对称轴在
,即a、b同号,对称轴在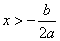 (或x>h)时,
(或x>h)时,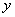 随
随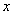 的增大而增大;
的增大而增大;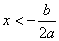 (或x<h)时,
(或x<h)时,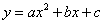 与
与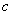 ),c值为抛物线在y轴上的截距.
),c值为抛物线在y轴上的截距.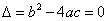 时,抛物线与x轴有一个交点;②
时,抛物线与x轴有一个交点;②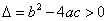 时,抛物线与x轴有两个交点;③
时,抛物线与x轴有两个交点;③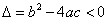 时,抛物线与x轴没有交点.
时,抛物线与x轴没有交点.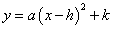 ,上加下减:
,上加下减: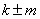 ;左加右减:
;左加右减: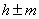
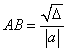 或
或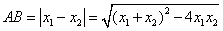
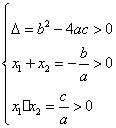 ;
;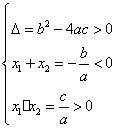 ;
;