<1>在等差数列
(这里即中,当项数为偶数);时,
。 ;项数为奇数时,,如(2)若等差数列、的前和分别为、,且,则.如设{}与
{}是两个等差数列,它们的前项和分别为和,若,那么___________(答:)
<2>“首正”的递减等差数列中,前项和的最大值是所有非负项之和;“首负”的递增等差数列中,前项和的最小值是所有非正项之和。法一:由不等式组确定出前多少项为非负(或非正);法二:因等差数列前项是关于的二次函
数,故可转化为求二次函数的最值,但要注意数列的特殊性
能求一般数列中的最大或最小项吗
如(1)等差数列(2)若
中,,。上述两种方法是运用了哪种数学思想?(函数思想),由此你,问此数列前多少项和最大?并求此最大值。(答:前13项和最大,最大值为169);,
成立的最大正整数n是 (答:4006) 是等差数列,首项,则使前n项和
<3> 若是等比数列,则、、成等比数列;若成等比数列,则、
成等比数列;若
时,数列
如①已
知
是等比数列,且公比
,则数列
,?也是等比数列。当,且为偶数 ,?是常数数列0,它不是等比数列。 且,设数
列满
足,
且,
则
. (答:
则的值为______(答:40)
<4>
如设等比数列的公比为,前。 项和为);②在等比数列中,为其前n项和,若,,若成等差数列,则的值为_____(答:-2)
<5>在等比数列中,当项数为偶数时,;项数为奇数时,。
如设数列的前项和为
(),
关于数列
有下列三个命题:①若
,则既是等差数列又是等比数列;②若真命题的序号是 (答:②③)
一.数列的通项的求法:
,则是等差数列;③若,则是等比数列。这些命题中,
⑴公式法:①等差数列通项公式;②等比数列通项公式。
…… …… 余下全文

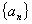 是递增数列,前n项和为
是递增数列,前n项和为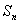 ,且
,且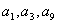 成等比数列,
成等比数列,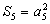 .求数列
.求数列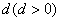
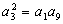 ,
,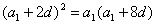
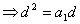
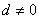 , ∴
, ∴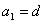 ………………………………①
………………………………①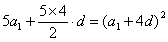 …………②
…………②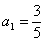 ,
,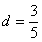
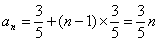
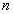 项和
项和 的关系,求数列
的关系,求数列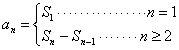 求解。
求解。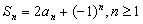 .求数列
.求数列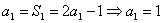
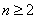 时,有
时,有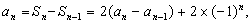
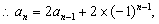
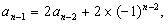 ……,
……,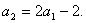
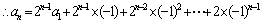
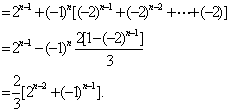
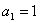 也满足上式,所以
也满足上式,所以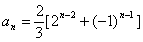
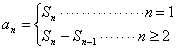 求解时,要注意对n分类讨论,但若能合写时一定要合并.
求解时,要注意对n分类讨论,但若能合写时一定要合并.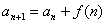
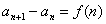 ,利用累加法(逐差相加法)求解。
,利用累加法(逐差相加法)求解。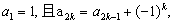
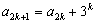 ,其中
,其中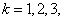 ……,求数列
……,求数列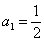 ,
,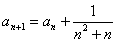 ,求
,求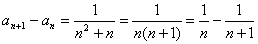
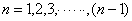 ,代入上式得
,代入上式得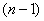 个等式累加之,即
个等式累加之,即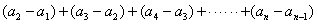
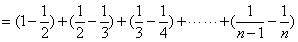
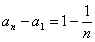
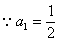 ,
,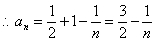
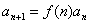
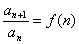 ,利用累乘法(逐商相乘法)求解。
,利用累乘法(逐商相乘法)求解。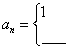
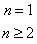 P24(styyj)
P24(styyj) 是递增数列,前n项和为
是递增数列,前n项和为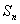 ,且
,且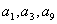 成等比数列,
成等比数列,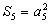 .求数列
.求数列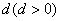
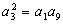 ,
,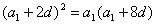
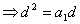
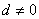 , ∴
, ∴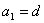 ………………………………①
………………………………①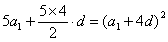 …………②
…………②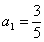 ,
,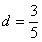
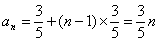
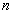 项和
项和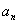 的关系,求数列
的关系,求数列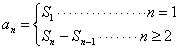 求解。
求解。 .求数列
.求数列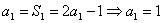
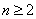 时,有
时,有
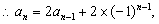
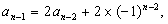 ……,
……,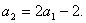
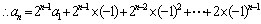
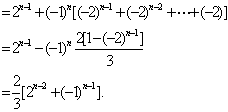
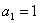 也满足上式,所以
也满足上式,所以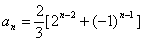
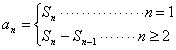 求解时,要注意对n分类讨论,但若能合写时一定要合并.
求解时,要注意对n分类讨论,但若能合写时一定要合并.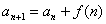
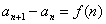 ,利用累加法(逐差相加法)求解。
,利用累加法(逐差相加法)求解。
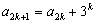 ,其中
,其中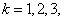 ……,求数列
……,求数列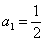 ,
,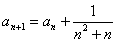 ,求
,求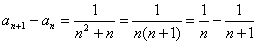
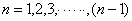 ,代入上式得
,代入上式得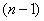 个等式累加之,即
个等式累加之,即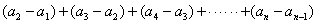
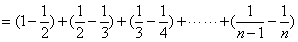
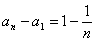
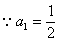 ,
,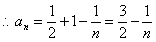
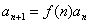
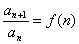 ,利用累乘法(逐商相乘法)求解。
,利用累乘法(逐商相乘法)求解。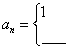
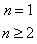 P24(styyj)
P24(styyj)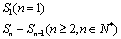 注意验证a1是否包含在an 的公式中.
注意验证a1是否包含在an 的公式中.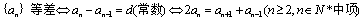
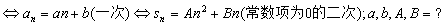
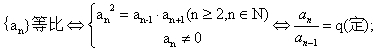
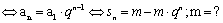
 是等比数列,且
是等比数列,且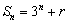 ,则
,则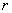 = (答:-1)
= (答:-1)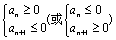 ,或用二次函数处理;(等比前n项积?),由此你能求一般数列中的最大或最小项吗?
,或用二次函数处理;(等比前n项积?),由此你能求一般数列中的最大或最小项吗? ,
,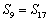 ,问此数列前多少项和最大?并求此最大值.(答:前13项和最大,最大值为169);
,问此数列前多少项和最大?并求此最大值.(答:前13项和最大,最大值为169);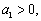
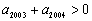 ,
,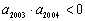 ,则使前n项和
,则使前n项和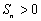 成立的最大正整数n是 (答:4006)
成立的最大正整数n是 (答:4006)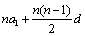 =
=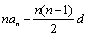 =
=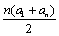
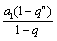 =
=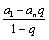
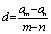 ;当m+n=p+q,am+an=ap+aq;
;当m+n=p+q,am+an=ap+aq;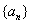 中,
中,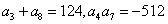 ,公比q是整数,则
,公比q是整数,则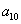 =___(答:512);
=___(答:512);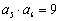 ,则
,则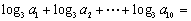 (答:10).
(答:10).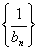 、{anbn}、
、{anbn}、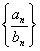 等比;
等比; (c>0)成等比.
(c>0)成等比.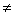 1)等差.
1)等差.
 项和为
项和为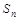 ,在
,在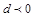 时,有最大值. 如何确定使
时,有最大值. 如何确定使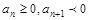 ,成立的
,成立的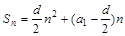 利用二次函数的性质求
利用二次函数的性质求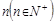 ,则
,则
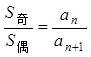 ;
;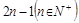 ,则
,则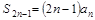 ,且
,且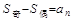 ,
,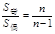
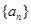 、
、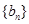 的前
的前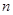 和分别为
和分别为 、
、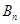 ,则
,则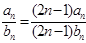 =
=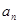 }与{
}与{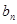 }是两个等差数列,它们的前
}是两个等差数列,它们的前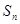 和
和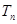 ,若
,若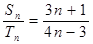 ,那么
,那么 ___________(答:
___________(答: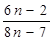 )
)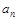 }的前
}的前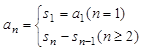
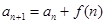 把原递推公式转化为
把原递推公式转化为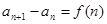 ,利用累加法(逐差相加法)求解
,利用累加法(逐差相加法)求解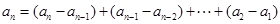
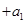
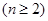 。
。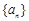 满足
满足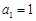 ,
,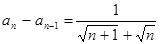
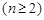 ,则
,则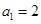 ,
,  ,则
,则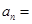
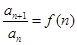 求
求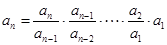
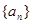 中,
中,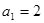 ,前
,前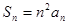 ,求
,求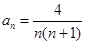 )设{an}的首项为1的正项数列,且
)设{an}的首项为1的正项数列,且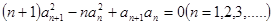 求它的通项公式。
求它的通项公式。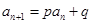 (为p,q为常数且
(为p,q为常数且 )的数列
)的数列 ,利用等比数列求出
,利用等比数列求出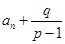 的表达式,进而求出
的表达式,进而求出
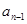
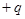 两式相减可得:
两式相减可得: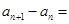
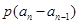 ,利用
,利用 成等比数列求出
成等比数列求出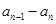 ,再利用迭代或迭加求出
,再利用迭代或迭加求出 ,先用累加法求
,先用累加法求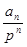 再求
再求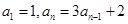 ,求
,求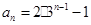 );
);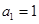 ,
,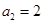 ,
,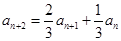 求
求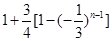 .)
.)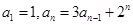 ,求
,求 );
);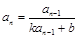 (
(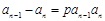 )(
)(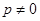 )的递推数列都可以用倒数法求通项。可化为
)的递推数列都可以用倒数法求通项。可化为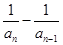 =
=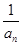 的表达式,再求
的表达式,再求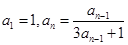 ,求
,求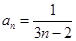 );
); =1,
=1,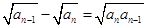 ,求
,求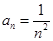 )
)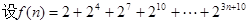

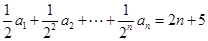 ,求
,求 ,且
,且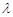 的取值范围(
的取值范围(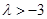 );
);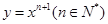 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为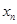 ,令
,令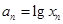 ,则
,则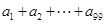 的值为 . (答案:-2)
的值为 . (答案:-2)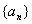 前
前 项和
项和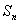 ,则
,则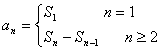 (注意:不能忘记讨论
(注意:不能忘记讨论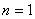 )
) 满足
满足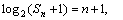 求此数列的通项公式。
求此数列的通项公式。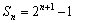 ,当
,当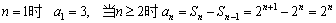
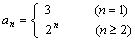
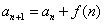 (
(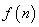 可以求和)
可以求和)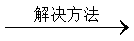 累加法
累加法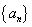 中,已知
中,已知 =1,当
=1,当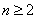 时,有
时,有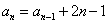
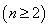 ,求数列的通项公式。
,求数列的通项公式。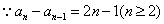
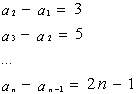 上述
上述 个等式相加可得:
个等式相加可得: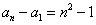
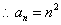
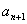 =
=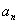 +3
+3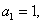
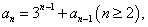 求通项公式
求通项公式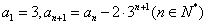 ,则求这个数列的通项公式
,则求这个数列的通项公式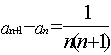 ,则求这个数列的通项公式
,则求这个数列的通项公式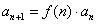 (
(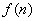 可以求积)
可以求积)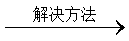 累积法
累积法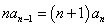 ,(
,(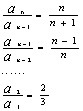
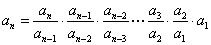
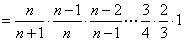
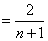
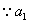 也满足上式;
也满足上式;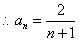

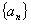 满足
满足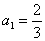 ,
,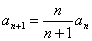 ,求
,求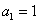 ,
,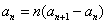
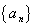 通项公式.
通项公式. ,求通项公式
,求通项公式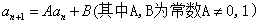
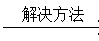 待定常数法
待定常数法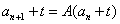 ,其中
,其中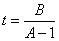 ,则数列
,则数列 为公比等于A的等比数列,然后求
为公比等于A的等比数列,然后求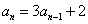 ,求数列
,求数列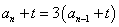 ,则
,则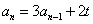
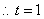 ,于是
,于是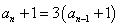
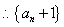 是以
是以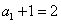 为首项,以3为公比的等比数列。
为首项,以3为公比的等比数列。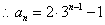
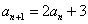 ,求数列
,求数列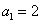 ,
,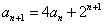 ,求
,求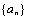 满足
满足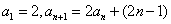 ,求通项
,求通项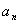
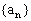 满足
满足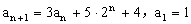 ,求数列
,求数列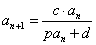 (
(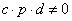 )
) 倒数法
倒数法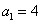 ,
,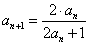 ,求
,求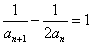 ,设
,设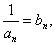 则
则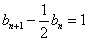 ;
; ;展开后得,
;展开后得,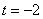 ;
;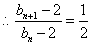 ;
;
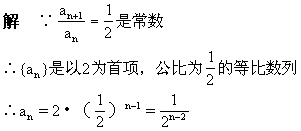 例2、已知
例2、已知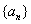 满足
满足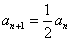 ,而
,而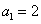 ,求
,求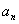 =?
=?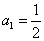 ,
,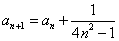 ,求
,求
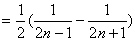
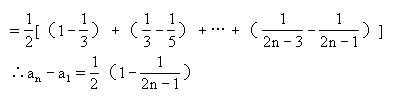
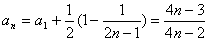
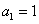 ,对于n>1(n∈N)有
,对于n>1(n∈N)有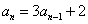 ,求
,求