导数大题方法总结
一总论
一般来说,导数的大题有两到三问。每一个小问的具体题目虽然并不固定,但有相当的规律可循,所以在此我进行了一个答题方法的总结。
二主流题型及其方法
*(1)求函数中某参数的值或给定参数的值求导数或切线
一般来说,一到比较温和的导数题的会在第一问设置这样的问题:若f(x)在x = k时取得极值,试求所给函数中参数的值;或者是f(x)在(a , f(a))处的切线与某已知直线垂直,试求所给函数中参数的值等等很多条件。虽然会有很多的花样,但只要明白他们的本质是考察大家求导数的能力,就会轻松解决。这一般都是用来送分的,所以遇到这样的题,一定要淡定,方法是:
先求出所给函数的导函数,然后利用题目所给的已知条件,以上述第一种情形为例:令x = k,f(x)的导数为零,求解出函数中所含的参数的值,然后检验此时是否为函数的极值。
注意:①导函数一定不能求错,否则不只第一问会挂,整个题目会一并挂掉。保证自己求导不会求错的最好方法就是求导时不要光图快,一定要小心谨慎,另外就是要将导数公式记牢,不能有马虎之处。②遇到例子中的情况,一道要记得检验,尤其是在求解出来两个解的情况下,更要检验,否则有可能会多解,造成扣分,得不偿失。所以做两个字来概括这一类型题的方法就是:淡定。别人送分,就不要客气。③求切线时,要看清所给的点是否在函数上,若不在,要设出切点,再进行求解。切线要写成一般式。
*(2)求函数的单调性或单调区间以及极值点和最值
一般这一类题都是在函数的第二问,有时也有可能在第一问,依照题目的难易来定。这一类题问法都比较的简单,一般是求f(x)的单调(增减)区间或函数的单调性,以及函数的极大(小)值或是笼统的函数极值。一般来说,由于北京市高考不要求二阶导数的计算,所以这类题目也是送分题,所以做这类题也要淡定。这类问题的方法是:
首先写定义域,求函数的导函数,并且进行通分,变为假分式形式。往下一般有两类思路,一是走一步看一步型,在行进的过程中,一点点发现参数应该讨论的范围,一步步解题。这种方法个人认为比较累,而且容易丢掉一些情况没有进行讨论,所以比较推荐第二种方法,就是所谓的一步到位型,先通过观察看出我们要讨论的参数的几个必要的临介值,然后以这些值为分界点,分别就这些临界点所分割开的区间进行讨论,这样不仅不会漏掉一些对参数必要的讨论,而且还会是自己做题更有条理,更为高效。
…… …… 余下全文

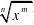
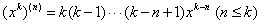 ;
;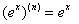 ;
;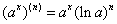 ;
;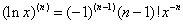 ;
;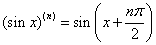 ;
;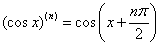 ;
;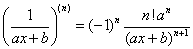 。
。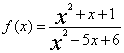 的n阶导数。
的n阶导数。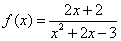
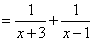 ,
,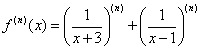
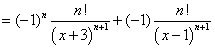 。
。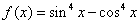 的n阶导数。
的n阶导数。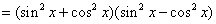
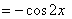 ;
;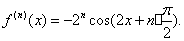
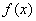 与
与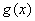 都是
都是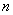 阶可导函数,则它们的积函数也
阶可导函数,则它们的积函数也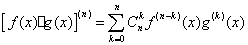
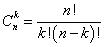 是组合系数。
是组合系数。